반응형
평면의 방정식은 아래와 같습니다.
ax + by + cz + d = 0
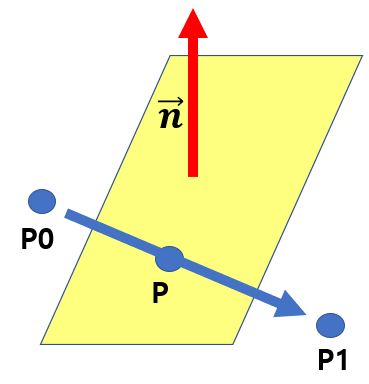
면의 방정식과 두 점을 아는 상태에서 평면과 만나는 두 점 사이의 점을 구하여 보겠습니다.
비율 r을 P – P0 / P1 – P0으로 정의하겠습니다. 비율 r을 구하기 위하여 분모 및 분자에 평면에 수직한 법선 벡터 n을 내적하면 비율 r은 아래와 같습니다. 참고로 벡터 n은 평면을 방정식을 응용하면 (a, b, c)가 됩니다.
r = P·벡터 n – P0 ·벡터 n / P1 ·벡터 n – P0 ·벡터 n
여기서 P는 평면과 교차함으로 평면내에 포함되어 있어 P·벡터 n은 평면의 방정식에 의하여 –d가 됩니다.
r과 관련된 수식에서 P의 값 만을 알 수 없었으므로 P·벡터 n을 –d값으로 치환하여 r을 구합니다.
P는 P0 + r * (P1 – P0)이 되므로 구한 r값과 아는 두 점 P0, P1의 값을 대입하여 구하면 됩니다.
다시 수식으로 요약하면 아래와 같습니다.
r = P·벡터 n – P0 ·벡터 n / P1 ·벡터 n – P0 ·벡터 n
P = P0 + r * (P1 – P0)
반응형
'3D 그래픽 프로그래밍' 카테고리의 다른 글
| 자체 3D 엔진만들 때 도움이 될 만한 무료 강의 (8) | 2024.09.22 |
|---|---|
| [서평] DirectX 12를 이용한 3D 게임 프로그래밍 입문 (0) | 2023.03.16 |
| [서평] DirectX 11을 이용한 3D 게임 프로그래밍 입문 (0) | 2023.01.15 |
| [서평] 이득우의 언리얼 C++ 게임 개발의 정석 (0) | 2022.12.29 |
| 세 점을 포함하는 평면의 방정식 구하기 (0) | 2021.11.16 |
| DirectX 관련 참고할 만한 역사 (1) | 2021.10.06 |
| 빌보드(Billboard) 구현하기 (0) | 2021.09.12 |
| 두 점 사이의 각도 구하기: atan2 (1) | 2021.09.12 |