DevMemo

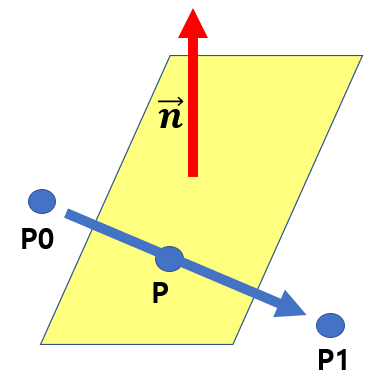
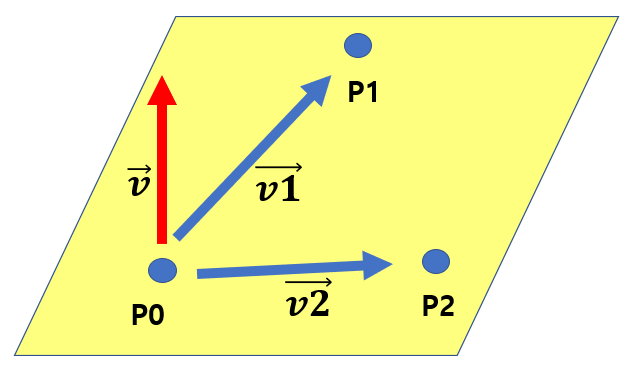
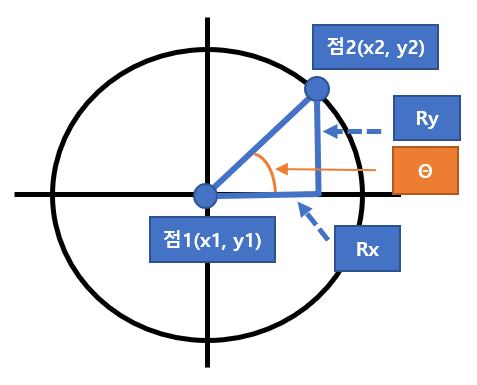
평면의 방정식은 아래와 같습니다. ax + by + cz + d = 0 면의 방정식과 두 점을 아는 상태에서 평면과 만나는 두 점 사이의 점을 구하여 보겠습니다. 비율 r을 P – P0 / P1 – P0으로 정의하겠습니다. 비율 r을 구하기 위하여 분모 및 분자에 평면에 수직한 법선 벡터 n을 내적하면 비율 r은 아래와 같습니다. 참고로 벡터 n은 평면을 방정식을 응용하면 (a, b, c)가 됩니다. r = P·벡터 n – P0 ·벡터 n / P1 ·벡터 n – P0 ·벡터 n 여기서 P는 평면과 교차함으로 평면내에 포함되어 있어 P·벡터 n은 평면의 방정식에 의하여 –d가 됩니다. r과 관련된 수식에서 P의 값 만을 알 수 없었으므로 P·벡터 n을 –d값으로 치환하여 r을 구합니다. P는 P0 + r ..

평면의 방정식은 아래와 같습니다. ax + by + cz + d = 0 평면이 세 점 P0, P1, P2를 그림과 같이 포함한다고 하겠습니다. 해당 세 점을 바탕으로 벡터 V1 = P1 – P0과 벡터 V2 = P2 – P0을 정의할 수 있습니다. 그리고 벡터 V1과 벡터 V2의 외적를 구한 후 정규화하여 벡터 V를 구할 수 있습니다. 이 때 벡터 V의 x, y, z은 평면의 방정식의 a, b, c가 됩니다. 구한 벡터 V에 P0을 내적하면 평면의 방정식에 의하여 0이 되어야 함으로 이를 바탕으로 아래와 같이 d를 구할 수 있습니다. 벡터 V·P0 + d = 0 d = - (벡터V·P0) 마지막으로 위에서 구한 a, b, c, d를 대입하여 평면을 방정식을 구하면 됩니다.

두 점 사이의 라디언 각도는 아크탄젠트라는 수학 함수를 통하여 구할 수 있다. 프로그래밍 함수로는 atan2(y의 차이, x의 차이)로 구할 수 있다. 아크탄젠트는 개념적으로 아래와 같이 라디언 각도를 구한다. 라디언 각도 Θ = atan(Ry / Rx) 프로그램밍 적으로는 atan2(y2-y1, x2-x1)으로 구할 수 있다. 인자를 보면 점2 – 점1으로 Rx와 Ry를 구하는 것을 알 수 있다.